POLEA
La polea es un dispositivo mecánico de tracción o elevación, formado por una rueda (también denominada roldana) montada en un eje, con una cuerda que rodea la circunferencia de la rueda.
Las grúas más simples con una sola rueda de poleas fueron inventadas hace unos 3.000 años, y las poleas compuestas con varias ruedas hacia el año 400 a.C. Se dice que Arquímides inventó la polea compuesta y fue capaz de levantar un barco y llevarlo a la costa.
Imagina que quieres levantar algo muy pesado y no tienes suficiente fuerza en tus músculos para hacerlo...¿cómo lo solucionarías?.
"Si queremos mover cualquier peso, atamos una cuerda a este peso y...tiramos de la cuerda hasta que lo levantamos. Para esto se necesita una fuerza igual al peso que deseamos levantar. Sin embargo, si desatamos la cuerda del peso y atamos un extremo en una sólida viga, pasamos el otro extremo por una polea que vaya sujeta al centro del peso, y tiramos de la cuerda, moveremos más fácilmente el peso."
Este relato del siglo III es una de las descripciones más antiguas y más claras de la diferencia entre polea fija y una polea movible.
La polea fija son aquellas que no cambian de sitio, solamente giran alrededor de su propio eje. Se usa, por ejemplo, para subir objetos a los edificios o sacar agua de los pozos. Una polea fija puede ser considerada como una palanca de primera clase. En las palancas de primer género el punto de apoyo se encuentra entre los extremos.
En cambio, las móviles, además de que giran alrededor de su eje, también se desplazan. En las poleas móviles el punto de apoyo está en la cuerda y no en el eje, por lo tanto puede presentar movimientos de traslación y rotación. Como el caso de dos personas que cargan una bolsa, cada una de ellas hace las veces de una polea y sus brazos las veces de cuerdas, el peso se reparte entre los dos y se produce una ventaja mecánica, reduciéndose el esfuerzo a la mitad. La polea móvil es una palanca de segunda clase.
Poleas simples: Sólo con una cuerda y una rueda se puede arreglar el cambio de dirección. Se fija la rueda a un soporte y se pasa una cuerda por la rueda hasta alcanzar la carga. Al tirar desde el otro extremo de la cuerda, se puede elevar la carga hasta la altura en que se halla fija la polea. El propio peso del cuerpo de la persona que tira se constituye en una ayuda.
Una rueda utilizada de esta manera, se convierte en una polea, y el sistema de elevación que realiza es una simple guía.
Las poleas simples se usan en máquinas en las que se debe cambiar la dirección del movimiento, como por ejemplo un ascensor.
Aquí, el movimiento ascendente de la cabina debe estar conectado con el movimiento descendente de un contrapeso.
En una polea ideal, la fuerza que se aplica para tirar de la cuerda es igual al peso de la carga. En la práctica, la fuerza es siempre un poco mayor, ya que tiene que vencer la fuerza de fricción en la rueda de la polea y elevar la carga.
Por ello, la fricción induce la eficacia de todas las máquinas.
En la polea simple la carga que se desea mover representa el peso o la fuerza de gravedad. Este tipo de polea se utiliza para sacar agua de un pozo, o para levantar una carga en una grúa.
Una polea simple es una palanca de primera clase. Sirve únicamente para cambiar de dirección o el sentido de la fuerza, ya que es más fácil ejercer tirando la cuerda hacia abajo que hacia arriba.

Poleas móviles: Esta polea se une a la carga y no a la viga. Una polea móvil simple es una palanca de segunda clase que multiplica la fuerza ejercida. La carga es soportada en igual magnitud por ambos segmentos de cuerda esto hace que la fuerza que es necesario aplicar disminuya a la mitad. Sin embargo, se debe tirar la cuerda a una distancia mayor.

Poleas Compuestas: Las poleas compuestas son aquellas donde se usan más de dos poleas en el sistema, y puede ser una fija y una móvil, o dos fijas y una móvil etc.,
Tirar una cuerda de arriba hacia abajo resulta más fácil que hacerlo desde bajo hacia arriba. Para cambiar la dirección del esfuerzo, a la polea móvil se agrega una polea fija.proporcionando una ventaja mecánica.
La ventaja mecánica es la disminución del esfuerzo

Esta ventaja mecánica la determinamos contando los segmentos de cuerda que llegan a las poleas móviles que soportan el esfuerzo.
La fuerza para levantar el cuerpo se va reduciendo proporcionalmente a la cantidad de segmentos de cuerda que soportan directamente la fuerza.
También podemos agregar a una polea otra polea fija o una o varias móviles para obtener una combinación de poleas que disminuya el esfuerzo.
Existen muchas combinaciones de poleas que se pueden usar, de acuerdo al trabajo que se deba realizar y la ventaja mecánica que se desea conseguir.
PALANCA
La palanca es una MAQUINA SIMPLE que se emplea en una gran variedad de aplicaciones. Está formada por una barra rígida que puede oscilar en torno a una pieza fija, que sirve de punto de apoyo. Cuando la fuerza se aplica en el extremo de la barra más alejado del punto de apoyo, la fuerza resultante en el extremo más próximo al punto de apoyo es mayor.
Los hombres primitivos gracias a su intuición se dieron cuenta de que las palancas, mecanismo usado en ondas, remos, etc., podían ayudarles a sacar mayor provecho de su fuerza muscular. Pero fue Arquímides (287-212 a.C), un científico de la antigua Grecia, quien logró explicar el funcionamiento de la palanca.
Ilustró su teoría con una frase muy famosa: "Dadme un punto de apoyo y moveré el mundo", dando por hecho que de tener una palanca suficientemente larga podría mover la Tierra con sus propias fuerzas.
Arquímides, basándose en dos principios, estableció las leyes de la palanca.
PRINCIPIO 1
"Si se tiene una palanca en cuyos extremos actúan pesos iguales, la palanca se equilibrará colocando el punto de apoyo en el medio de ella."
PINCIPIO 2
"Un peso se puede descomponer en dos mitades actuando a igual distancia del punto medio de la palanca".
PERO...¿QUÉ SON REALMENTE LAS PALANCAS?
Se define a la palanca como una barra rígida apoyada en un punto sobre la cual se aplica una fuerza pequeña para obtener una gran fuerza en el otro extremo; la fuerza pequeña se denomina "potencia" (p) y la gran fuerza, "resistencia" (R), al eje de rotación sobre el cual gira la palanca se llama "punto de apoyo" o "fulcro" (A).
Al utilizar palancas se aplica el principio de los momentos donde una de las fuerzas hace girar la palanca en un sentido y la otra en sentido contrario.
TIPO DE PALANCAS:
De acuerdo con la posición de la "potencia" y de la "resistencia" con respecto al "punto de apoyo", se consideran tres clases de palancas, que son:
- En el primer tipo el punto de apoyo se ubica entre la carga y la fuerza aplicada. Mientras mas cerca esta de la carga entonces la fuerza aplicada puede ser menor. Es nuestra idea intuitiva de palanca, algo que nos ayuda a mover una carga pesada
- En el segundo tipo el punto de apoyo esta en un extremo del brazo, la carga se ubica en la parte mas cercana al punto de apoyo y la fuerza aplicada en la lejana. De esta forma funciona una carretilla. Su utilidad es evidente, mientras mas cerca este la carga en la carretilla del punto de apoyo, (la rueda), mas sencillo es desplazarla.
En el tercer tipo, el punto de apoyo sigue en uno de los extremos, pero invertimos las posiciones relativas de la carga y la fuerza aplicada. Como la carga esta mas alejada del punto de apoyo la fuerza aplicada debe ser mayor. En contraste la carga tiene un gran movimiento. De este tipo son las palancas que funcionan en las articulaciones de los brazos por ejemplo. Con independencia del tipo de palanca, la ventaja mecánica se calcula de la misma manera. Sólo hay que considerar el valor de ambas fuerzas y el brazo de cada una de ellas (definido como la distancia entre el punto de apoyo y el punto de aplicación de la fuerza).
Para que exista equilibrio, los momentos de ambas fuerzas deben ser iguales, de manera que
F resistente R resistente = F aplicada R aplicada
donde
F resistente : fuerza resistente
R resistente : brazo de la fuerza resistente
F aplicada : fuerza aplicada
R aplicada : brazo de la fuerza aplicada
Por lo que respecta a la ventaja mecánica,
A = R aplicada / R resistente
LEYES DE NEWTON
Primera ley de Newton o Ley de la inercia
La primera ley del movimiento rebate la idea aristotélica de que un cuerpo sólo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que:
Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él.
Esta ley postula, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilineo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuyo resultante no sea nulo sobre él. Newton toma en cuenta, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como esta a la fricción.
En consecuencia, un cuerpo con movimiento rectilíneo uniforme implica que no existe ninguna fuerza externa neta o, dicho de otra forma, un objeto en movimiento no se detiene de forma natural si no se aplica una fuerza sobre él. En el caso de los cuerpos en reposo, se entiende que su velocidad es cero, por lo que si esta cambia es porque sobre ese cuerpo se ha ejercido una fuerza neta.
Ejemplo, para un pasajero de un tren, el interventor viene caminando lentamente por el pasillo del tren, mientras que para alguien que ve pasar el tren desde el andén de una estación, el interventor se está moviendo a una gran velocidad. Se necesita, por tanto, un sistema de referencia al cual referir el movimiento.
La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como Sistemas de referencia inerciales, que son aquellos sistemas de referencia desde los que se observa que un cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad constante.
En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial. En muchos casos, por ejemplo, suponer a un observador fijo en la Tierra es una buena aproximación de sistema inercial.
Segunda ley de Newton o Ley de fuerza
La segunda ley del movimiento de Newton dice que
El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.
Esta ley explica qué ocurre si sobre un cuerpo en movimiento (cuya masa no tiene por qué ser constante) actúa una fuerza neta: la fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. En concreto, los cambios experimentados en el momento lineal de un cuerpo son proporcionales a la fuerza motriz y se desarrollan en la dirección de esta; esto es, las fuerzas son causas que producen aceleraciones en los cuerpos. Consecuentemente, hay relación entre la causa y efecto, esto es, la fuerza y la aceleración están relacionadas. Dicho sintéticamente, la fuerza se define simplemente en función del momento en que se aplica a un objeto, con lo que dos fuerzas serán iguales si causan la misma tasa de cambio en el momento del objeto.
En términos matemáticos esta ley se expresa mediante la relación:
Donde  es el momento lineal y es el momento lineal y  la fuerza total. Si suponemos la masa constante y nos manejamos con velocidades que no superen el 10% de la velocidad de la luz podemos reescribir la ecuación anterior siguiendo los siguientes pasos: la fuerza total. Si suponemos la masa constante y nos manejamos con velocidades que no superen el 10% de la velocidad de la luz podemos reescribir la ecuación anterior siguiendo los siguientes pasos:
Sabemos que  es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad. es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.
Consideramos a la masa constante y podemos escribir  aplicando estas modificaciones a la ecuación anterior: aplicando estas modificaciones a la ecuación anterior:
que es la ecuación fundamental de la dinámica, donde la constante de proporcionalidad, distinta para cada cuerpo, es su masa de inersia. Veamos lo siguiente, si despejamos m de la ecuación anterior obtenemos que m es la relación que existe entre  y y 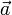 . Es decir la relación que hay entre la fuerza aplicada al cuerpo y la aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a cambiar su aceleración (una gran masa) se dice que tiene mucha inercia. Es por esta razón por la que la masa se define como una medida de la inercia del cuerpo. . Es decir la relación que hay entre la fuerza aplicada al cuerpo y la aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a cambiar su aceleración (una gran masa) se dice que tiene mucha inercia. Es por esta razón por la que la masa se define como una medida de la inercia del cuerpo.
Por tanto, si la fuerza resultante que actúa sobre una partícula no es cero, esta partícula tendrá una aceleración proporcional a la magnitud de la resultante y en dirección de ésta. La expresión anterior así establecida es válida tanto para la mecanica clasica como para la mecanica relativista, a pesar de que la definición de momento lineal es diferente en las dos teorías: mientras que la dinámica clásica afirma que la masa de un cuerpo es siempre la misma, con independencia de la velocidad con la que se mueve, la mecánica relativista establece que la masa de un cuerpo aumenta al crecer la velocidad con la que se mueve dicho cuerpo.
De la ecuación fundamental se deriva también la definición de la unidad de fuerza o newton. Si la masa y la aceleración valen 1, la fuerza también valdrá 1; así, pues, el newton es la fuerza que aplicada a una masa de un kilogramo le produce una aceleración de 1 m/s². Se entiende que la aceleración y la fuerza han de tener la misma dirección y sentido.
La importancia de esa ecuación estriba sobre todo en que resuelve el problema de la dinámica de determinar la clase de fuerza que se necesita para producir los diferentes tipos de movimiento: rectilíneo uniforme (m.r.u), circular uniforme (m.c.u) y uniformemente acelerado (m.r.u.a).
Si sobre el cuerpo actúan muchas fuerzas, habría que determinar primero el vector suma de todas esas fuerzas. Por último, si se tratase de un objeto que cayese hacia la tierra con una resistencia del aire igual a cero, la fuerza sería su peso, que provocaría una aceleración descendente igual a la de la gravedad.
Tercera ley de Newton o Ley de acción y reacción
Con toda acción ocurre siempre una reacción igual y contraria: o sea, las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto.
La tercera ley es completamente original de Newton (pues las dos primeras ya habían sido propuestas de otras maneras por galileo, hookey, hungesrt) y hace de las leyes de la mecánica un conjunto lógico y completo. Expone que por cada fuerza que actúa sobre un cuerpo, este realiza una fuerza de igual intensidad, pero de sentido contrario sobre el cuerpo que la produjo. Dicho de otra forma, las fuerzas, situadas sobre la misma recta, siempre se presentan en pares de igual magnitud y de dirección, pero con sentido opuesto.
Este principio presupone que la interacción entre dos partículas se propaga instantáneamente en el espacio (lo cual requeriría velocidad infinita), y en su formulación original no es válido para fuerzas electromagnéticas puesto que estas no se propagan por el espacio de modo instantáneo sino que lo hacen a velocidad finita "c".
Es importante observar que este principio de acción y reacción relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas. Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley. Junto con las anteriores leyes, ésta permite enunciar los principios de conservacion del momento lineal y del momento angular
FISICOS RECONOCIDOS
Newton comparte con Leibniz el crédito por el desarrollo del cálculo integral y diferencial, que utilizó para formular sus leyes de la física. También contribuyó en otras áreas de lamatemática, desarrollando el teorema del binomio y las fórmulas de Newton-Cotes.
Entre sus hallazgos científicos se encuentran el descubrimiento de que el espectro de color que se observa cuando la luz blanca pasa por un prisma es inherente a esa luz, en lugar de provenir del prisma (como había sido postulado por Roger Bacon en el siglo XIII); su argumentación sobre la posibilidad de que la luz estuviera compuesta por partículas; su desarrollo de una ley de convección térmica, que describe la tasa de enfriamiento de los objetos expuestos al aire; sus estudios sobre la velocidad del sonido en el aire; y su propuesta de una teoría sobre el origen de las estrellas. Fue también un pionero de lamecánica de fluidos, estableciendo una ley sobre la viscosidad.
Newton fue el primero en demostrar que las leyes naturales que gobiernan el movimiento en la Tierra y las que gobiernan el movimiento de los cuerpos celestes son las mismas. Es, a menudo, calificado como el científico más grande de todos los tiempos, y su obra como la culminación de la revolución científica. El matemático y físico matemático Joseph Louis Lagrange (1736–1813), dijo que "Newton fue el más grande genio que ha existido y también el más afortunado dado que sólo se puede encontrar una vez un sistema que rija el mundo."
GALILEO:
un astrónomo, filósofo, matemático y físico italiano que estuvo relacionado estrechamente con la revolución científica. Eminente hombre del Renacimiento, mostró interés por casi todas las ciencias y artes (música, literatura, pintura). Sus logros incluyen la mejora deltelescopio, gran variedad de observaciones astronómicas, la primera ley del movimiento y un apoyo determinante para el copernicanismo. Ha sido considerado como el «padre de la astronomía moderna», el «padre de la física moderna»6 y el «padre de la ciencia».
Su trabajo experimental es considerado complementario a los escritos de Francis Bacon en el establecimiento del moderno método científico y su carrera científica es complementaria a la de Johannes Kepler. Su trabajo se considera una ruptura de las teorías asentadas de la física aristotélica y su enfrentamiento con la Inquisición romana de la Iglesia Católica Romana suele presentarse como el mejor ejemplo de conflicto entre religión y ciencia en la sociedad occidental.
KEPLER:
Las leyes de Kepler fueron enunciadas por Johannes Kepler para describir matemáticamente el movimiento de los planetas en sus órbitas alrededor del Sol. Aunque él no las enunció en el mismo orden[cita requerida], en la actualidad las leyes se numeran como sigue:
- Primera ley (1609): todos los planetas se desplazan alrededor del Sol siguiendo órbitas elípticas. El Sol está en uno de los focos de la elipse.
- Segunda ley (1609): el radio vector que une un planeta y el Sol barre áreas iguales en tiempos iguales.
La ley de las áreas es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio). En el afelio y en el perihelio, el momento angular L es el producto de la masa del planeta, su velocidad y su distancia al centro del Sol.
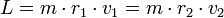
- Tercera ley (1618): para cualquier planeta, el cuadrado de su período orbital es directamente proporcional al cubo de la longitud del semieje mayor de su órbita elíptica.

Donde, T es el periodo orbital (tiempo que tarda en dar una vuelta alrededor del Sol), (L) la distancia media del planeta con el Sol y K la constante de proporcionalidad.
Estas leyes se aplican a otros cuerpos astronómicos que se encuentran en mutua influencia gravitatoria, como el sistema formado por la Tierra y la
Luna.
ROBERT HOOKE:
Físico y astrónomo inglés. En 1655 Robert Hooke colaboró con Robert Boyle en la construcción de una bomba de aire. Cinco años más tarde formuló la ley de la elasticidad que lleva su nombre, que establece la relación de proporcionalidad directa entre el estiramiento sufrido por un cuerpo sólido y la fuerza aplicada para producir ese estiramiento. En esta ley se fundamenta el estudio de la elasticidad de los materiales. Hooke aplicó sus estudios a la construcción de componentes de relojes. En 1662 fue nombrado responsable de experimentación de la Royal Society de Londres, siendo elegido miembro de dicha sociedad al año siguiente.

Robert Hooke
En 1664, con un telescopio de Gregory de construcción propia, Robert Hooke descubrió la quinta estrella del Trapecio, en la constelación de Orión; así mismo fue el primero en sugerir que Júpiter gira alrededor de su eje. Sus detalladas descripciones del planeta Marte fueron utilizadas en el siglo XIX para determinar su velocidad de rotación.
Un año más tarde fue nombrado profesor de geometría en el Gresham College. Ese mismo año publicó Robert Hooke su obra Micrographia, en la cual incluyó estudios e ilustraciones sobre la estructura cristalográfica de los copos de nieve y discusiones sobre la posibilidad de manufacturar fibras artificiales mediante un proceso similar al que siguen los gusanos de seda. Los estudios de Hooke sobre fósiles microscópicos le llevaron a ser uno de los primeros impulsores de la teoría de la evolución de las especies.
|